이진트리(Binary Tree)
: 노드가 왼쪽 자식(left chile)과 오른쪽 자식(right child)만 가진다. 자식이 없을 수도 있다.
(최대 두 개의 자식 노드를 가지는 트리 형태의 자료구조로서, 단순히 값을 저장하기 위한 용도로 사용되기 보다는 효율적인 탐색 혹은 정렬을 위해 사용된다.)

완전 이진 트리(Complete Binary Tree)
- 마지막 레벨을 제외하고, 모든 레벨에 노드가 가득 찬다.
- 마지막 레벨은 왼쪽부터 채우고 끝까지 꽉 차지 않아도 된다.
- Heap, 우선순위 큐에서 사용하는 트리 구조이다.
* 힙(Heap): 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진 트리(complete binary tree)를 기본으로 한 자료구조이다.

이진 검색 트리(Binary Search Tree)
: 이진 검색(탐색)이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 이진 탐색과 연결리스트(linked list)를 결합한 자료구조의 일종이다. 다음 조건을 만족해야한다.

1. 왼쪽 서브트리(자식) 노드의 키값은 자기 자신의 노드 키값보다 작아야 한다. (왼쪽 자식 노드 < 부모 노드)
2. 오른쪽 서브트리(자식) 노드의 키값은 자기 자신의 노드 키값보다 커야한다. (오른쪽 자식 노드 > 부모 노드)
* 위의 두 경우를 만족하려면 키 값이 같은 노드는 복수로 존재할 수 없게 된다.
요약 : 이진 검색 트리의 특징 => [왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드]
- 이진 검색 트리를 중위 순회 DFS 스캔 시 키 값을 오름차순으로 얻게 된다.
1 => 4 => 5 => 6 => 7 => 9 => 11 => 12 => 13 => 14 => 15 => 18
- 이진 검색 트리는 평균 O(logN)의 시간복잡도를 가지며 트리가 한쪽으로 치우친 최악의 경우 O(N)의 시간복잡도를 가진다.
- 장점 🤗👍
1) 구조가 단순! simple
2) 중위 순회 DFS시 노드 값을 오름차순으로 얻을 수 있음 ! sorted
3) 이진 검색과 비슷한 방식으로 아주 빠르게 스캔 가능 ! fast
4) 노드 삽입이 쉬움 ! easily insert
이진 검색 트리 클래스 구현 (Binary Search Tree)
class Node
(1) 클래스 정의, 초기화
이진 탐색 트리를 구현하려면 먼저 그 재료가 되는 Node 클래스를 정의해야한다.
('노드'라는 느낌이 안 와서 간략히 정리해놓은 글)
[Python] 노드(Node) - 자료구조 기본 단위
노드 관리할 데이터를 보관(존재)하는 곳을 노드(Node)라고 한다. 즉, 자료구조에서 관리하고 있는 정보들 중 하나를 저장하고 있는 단위이다. 주로 연결 리스트라고 불리는 링크드 리스트에서 사
bo5mi.tistory.com
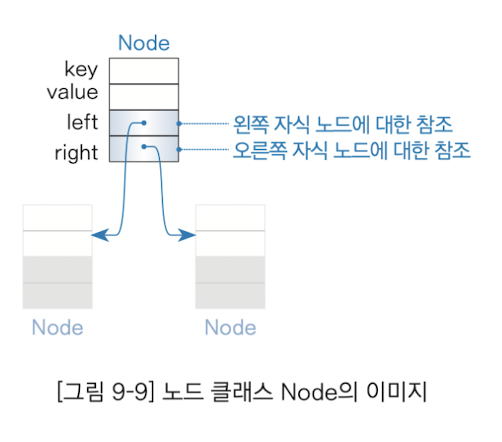
1. key(키)
2. value(자기 자신 노드의 값)
왜 key, value를 나눴을까, class Node의 저의(?)는 무엇인가 !?
일단, value는 key 따라다니는 애라고 느낌적으로 생각한다. 트리 구조 유지에 사용하는 건 바로 key이다.
* key와 value의 느낌을 받아들이기
=> 우선순위 큐에서 maxheap을 사용하기 위해 (-num, num) 형태로 push를 해주는데, 이때 -num이 key 역할은 하는 것이다. int값만을 push해서 사용했을 때는 그 숫자값이 key이자 동시에 value 역할을 했던 것이다.
3. left(왼쪽 자식 노드에 대한 참조 => 포인터를 이용)
4. right(오른쪽 자식 노드에 대한 참조 => 포인터를 이용)
굳이굳이 이진 검색 트리를 포인터로 만들어야 할 이유가 있을까? 당연히 있다.
노드 간 연결은 포인터로 나타낸다. 이중 연결 리스트는 노드당 2개의 포인터(다음/이전 노드 포인터)가 있다. 트리 역시 포인터가 2개 있는데, 각각 좌측, 우측 자식 노드를 가리킨다.
- 이진 탐색의 경우 탐색에 소요되는 계산 복잡성은 O(logN)으로 빠르지만, 자료 입력이나 삭제가 쉽지 않다.
- 연결 리스트의 경우 자료 입력, 삭제에 필요한 계산 복잡성은 O(1)로 효율적이지만, 탐색하는데에는 O(n)의 계산 복잡성이 발생한다.
=> 이중 연결 리스트와 이진 탐색의 장점을 살려보는 것이 이진 탐색 트리의 목적이라고 할 수 있다.
# class Node 코드
class Node:
# 이진 검색 트리의 노드
def __init__(self, key, value, left, right):
# 생성자(constructor)
self.key = key # 키
self.value = value # 값
self.left = left # 왼쪽 자식 포인터
self.right = right # 오른쪽 자식 포인터class BinarySearchTree
- __init__(): root에 None 대입 (노드가 하나도 없는 빈 트리 생성)
- search(): 루트에서 시작하여 키의 대소관계에 따라 왼쪽 또는 오른쪽 서브트리로 검색
- add(): 노드 삽입
- remove(): 노드 삭제
- dump(): 모든 노드를 키의 오름차순 또는 내림차순으로 출력
- min_key()와 max_key(): 가장 작은 키, 가장 큰 키를 찾아 반환
이제 Node 클래스를 사용해 이진 탐색 트리 클래스인 BinarySearchTree를 구현한다. 처음에는 비어 있는 트리이다.
class BinarySearchTree:
# 생성자
def __init__(self):
self.root = None # 트리의 root를 세팅한다. 초기에는 아무값도 넣지 않았으니 빈값으로 둔다.이제 여기에 원소를 추가, 삭제, 탐색할 수 있도록 insert(), delete(), find() 메서드를 추가해야한다.
class BinarySearchTree:
# 이진 검색 트리
def __init__(self):
# 초기화
self.root = None # root
# 노드가 하나도 없는 빈 트리 생성
def search(self, key: Any) -> Any:
# 키가 key 인 노드를 검색
p = self.root # 루트에 주목
while True:
if p is None: # 더 이상 진행할 수 없으면
return None # 검색 실패
if key == p.key: # key 와 노드 p 의 키가 같으면
return p.value # 검색 성공
elif key < p.key: # key쪽이 작으면
p = p.left # 왼쪽 서브트리에서 검색
else: # key쪽이 크면
p = p.right # 오른쪽 서브트리에서 검색
def add(self, key: Any, value: Any) -> bool:
# 키가 key이고 값이 value인 노드 삽입
def add_node(node: Node, key: Any, value: Any) -> None:
# node 를 루트로 하는 서브트리에 키가 key, 값이 value인 노드를 삽입
if key == node.key:
return False # key 가 이진검색트리에 이미 존재하면 False. 삽입 실패
elif key < node.key:
if node.left is None: # 왼쪽 자식 노드 없으면
node.left = Node(key, value, None, None) # 그 자리에 노드 삽입. 종료
else:
add_node(node.left, key, value) # 왼쪽 자식 노드 있으면 주목 노드 이동
else:
if node.right is None:
node.right = Node(key, value, None, None)
else:
add_node(node.right, key, value)
return True
if self.root is None: # 빈 트리에 삽입 시도 하면
self.root = Node(key, value, None, None) # 삽입되는 애 노드로 생성해줌 걔는 지가 루트고 혼자 존재하는 트리 그 자체
return True
else: # 빈 트리 아니면 위에서 만든 함수로 트리에 노드 추가
return add_node(self.root, key, value)
def remove(self, key: Any) -> bool:
# 키가 key인 노드를 삭제
p = self.root # 스캔 중인 노드
parent = None # 스캔 중인 노드의 부모 노드
is_left_child = True # p는 parent의 왼쪽 자식인지 확인
while True:
if p is None: # 더 이상 진행할 수 없으면
return False # 그 키는 존재하지 않음
if key == p.key: # key와 노드 p의 키가 같으면
break # 검색 성공
else:
parent = p # 가지를 내려가기 전에 부모로 현재 노드 설정. 스캔위치 자식으로 내려가면 현재 노드가 부모가 될거에요
if key < p.key: # key쪽이 작으면
is_left_child = True # 왼쪽 자식으로 가요
p = p.left # 왼쪽 서브트리에서 검색
else:
is_left_child = False # 여기서는 오른쪽 자식으로 가요
p = p.right # 오른쪽 서브트리로 스캔 고
if p.left is None: # p에 왼쪽 자식이 없으면
if p is self.root: # 근데 찾으려고 한 노드가 루트에 있었던 거면
self.root = p.right # 그러면 루트가 없어질거니까 새루트로 p오른쪽 자식
elif is_left_child: # p는 p.left 에서 온거 맞음 지금 parent 가 원래 p였음 = True
parent.left = p.right # p부모의 왼쪽 포인터가 p의 오른쪽 자식을 가리킴
else:
parent.right = p.right # p부모의 오른쪽 포인터가 p의 오른쪽 자식을 가리킴
elif p.right is None: # p에 오른쪽 자식이 없으면
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left # p부모의 왼쪽 포인터가 p왼쪽 자식을 가리킴
else:
parent.right = p.left # p부모의 오른쪽 포인터가 p왼쪽 자식을 가리킴
else: # p에 왼쪽 자식 있으면
parent = p
left = p.left
is_left_child = True
while left.right is not None: # 왼쪽 서브트리에서 가장 큰 키 찾기
parent = left
left = left.right # 온쪾 서브브트리에서 오른쪾 자식으로 계속 타고 내려감
is_left_child = False
p.key = left.key # 왼쪽 서브트리에서 가장 큰 키 복사해오기
p.value = left.value # 그 키의 값도 복사해와
if is_left_child:
parent.left = left.left # 원래 꺼랑 연결 끊고 복사해온 키로 부모랑 새로 연결해주기
else:
parent.right = left.left
return True
def dump(self, reverse = False) -> None:
# 덤프 (모든 노드를 키의 오름차순으로 출력)
def print_subtree(node: Node):
# node를 루트로 하는 서브트리의 노드를 키의 오름차순으로 출력
if node is not None:
print_subtree(node.left) # 왼족 서브트리를 오름차순으로 출력
print(f'{node.key} {node.value}') # node를 출력
print_subtree(node.right) # 오른쪽 서브트리를 오름차순으로 출력
def print_subtree_rev(node: Node):
# reverse 인자 False 로 들어오면 내림차순으로 출력
if node is not None:
print_subtree_rev(node.right) # 오른쪽 서브트리 내림차순으로 출력
print(f'{node.key} {node.value}') # node 출력
print_subtree_rev(node.left) # 왼쪽 서브트리 내림차순으로 출력
print_subtree(self.root) if reverse else print_subtree(self.root)
def min_key(self) -> Any:
# 가장 작은 키 찾아서 왼쪽으로 세상끝까지 따라가기
if self.root is None:
return None
p = self.root
while p.left is not None:
p = p.left
return p.key
def max_key(self) -> Any:
# 가장 큰 키 찾아요
if self.root is None:
return None
p = self.root
while p.right is not None:
p = p.right
return p.key1. 5639: 이진 탐색 트리
문제
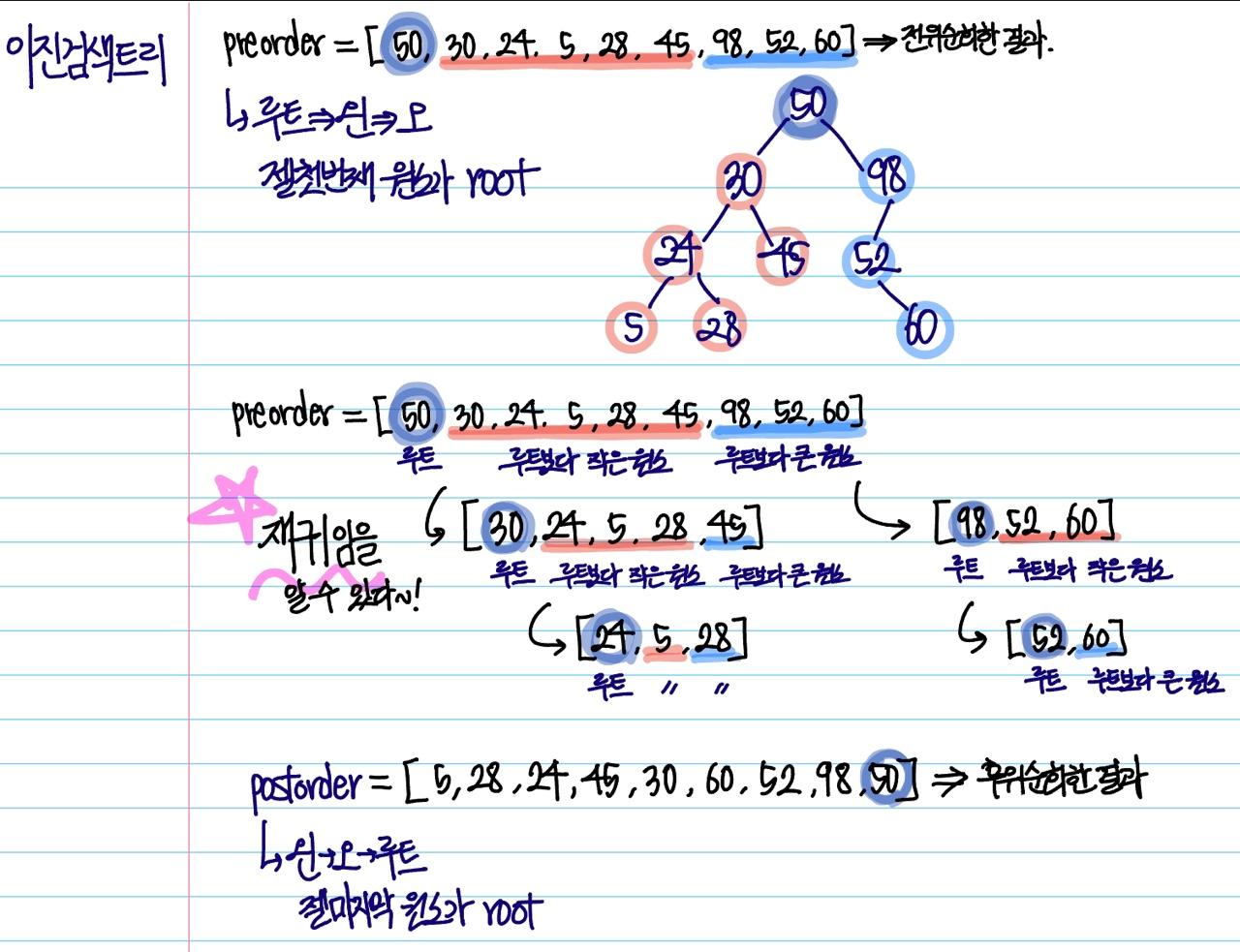
1. 이진 검색 트리에서 전위 순회(루트=>왼쪽=>오른쪽)한 값을 순서대로 입력
2. 입력 종료 조건이 없음(입력 크기가 정해져있지 않음)
3. 입력 값을 이용하여 후위순회(왼쪽=>오른족=>루트)한 값으로 출력
# 5639: 이진 검색 트리
# 노드의 왼쪽 서브 트리에 있는 모든 노드의 키는 노드의 키보다 작다.
# 노드의 오른쪽 서브 트리에 있는 모든 노드의 키는 노드의 키보다 크다.
# 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
# 출력: 입력으로 주어진 이진 검색 트리를 후위 순회한 결과 출력하라 ~!
import sys
sys.stdin = open("RETRY/이진검색트리/input.txt","r")
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def postorder(start, end):
# start와 end는 arr의 시작 idxd와 끝 idx임.
if start > end:
return
# 순회는 재귀호출을 통해 자식노드를 순회하기 때문에 자식노드의 여부를 확인하여야함.
root = preorder[start]
idx = start + 1
while idx <= end:
if preorder[idx] > root:
break
idx += 1
# preorder의 특징은 root > left > right 순으로 순회한다.
# binary search tree의 특징은 left child는 root보다 작은 value가 들어가며 right child는 root보다 큰 숫자가 들어간다는 점이다.
# 이러한 점을 이용하여 list에서 root보다 큰 숫자가 위치한 idx가 어디인지 확인할 수 있다.
postorder(start+1, idx-1)
postorder(idx, end)
print(root)
# 문제에서 요구하는 것은 입력으로 주어진 이진 검색 트리를 후위순회하는 것이다.
# 해당 함수는 root와 left, right를 구분했고 해당 함수를 left, right, root 순으로 다시 호출하여, 후위 순회를 완료하게 된다.
preorder = [] # 트리를 전위 순회한 결과 주어짐
while True: # 입력받는 값만 알고 입력의 개수를 모를 때
try:
preorder.append(int(input()))
except:
break
# 입력되는 값의 개수가 정해지지 않았기 때문에 반복문을 통해서 값을 리스트로 입력받게 될 경우 별도의 종료 조건을 설정하여야함.
# 예외처리를 하지 않으면 ValueError: invalid literal for int() with ~~ 가 발생되며 스크립트 실행이 중단됨.
# 따라서 이를 방지하기 위해 예외가 발생했을 때(except) 반복문을 종료하여 스크립트가 계속 실행되도록 함.
postorder(0, len(preorder)-1)# 5639: 이진 검색 트리
# 노드의 왼쪽 서브 트리에 있는 모든 노드의 키는 노드의 키보다 작다.
# 노드의 오른쪽 서브 트리에 있는 모든 노드의 키는 노드의 키보다 크다.
# 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
# 출력: 입력으로 주어진 이진 검색 트리를 후위 순회한 결과 출력하라 ~!
import sys
sys.stdin = open("RETRY/이진검색트리/input.txt","r")
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def postorder(preorder):
if len(preorder) == 1: # 마지막 노드인 것
print(preorder[0])
return
if len(preorder) == 0: # 혹시 빈 배열이 걸린다면 아무것도 하지 않는다.
return
divider = 0
root = preorder[0]
for i in range(1, len(preorder)):
if preorder[i] > root:
divider = i
break
if divider:
postorder(preorder[1:divider]) # 왼쪽 자식 노드
postorder(preorder[divider:]) # 오른쪽 자식 노드
print(preorder[0]) # 루트
else:
postorder(preorder[1:])
print(preorder[0])
preorder = []
while True:
try:
preorder.append(int(input()))
except:
break
postorder(preorder)2. 5639: 트리의 순회 => 다시 해보기/모르겠다..
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복없이 매겨져 있다.
이진트리의 인오더(중위순회)와 포스트오더(후위순회)가 주어졌을 때, 프리오더(전위순회)를 구하는 프로그램을 작성하시오.
이 문제 나와있는 예제가 진짜 별로다.....
중위 순회 : 7 3 8 1 9 4 10 0 11 5 2 6
후위 순회 : 7 8 3 9 10 4 1 11 5 6 2 0
후위 순회는 최상위 루트를 맨 마지막에 방문하며,
중위 순회는 왼쪽 서브 트리, 오른쪽 서브 트리 순으로 방문한다.
따라서, 후위 순회의 맨 마지막 원소는 최상위 루트이며,
이를 기준으로 중위 순회를 나누면, 왼쪽은 왼쪽 서브 트리, 오른쪽은 오른쪽 서브 트리임을 알 수 있다.
중위 순회 : 7 3 8 1 9 4 10 0 11 5 2 6
후위 순회 : 7 8 3 9 10 4 1 11 5 6 2 0
이때 중위 순회에서 왼쪽 서브 트리의 범위는
시작 인덱스 ~ (시작 인덱스 + 왼쪽 서브 트리의 노드 수 -1)
ex) 0(시작인덱스) ~ 0+7-1(시작 인덱스 + 왼쪽 서브 트리의 노드 수 -1) = 0 ~ 6
중위 순회에서 오른쪽 서브 트리의 범위는
(끝 인덱스 - 오른쪽 서브 트리의 수 +1) ~ 끝 인덱스
ex) 12-5+1(끝 인덱스 - 오른쪽 서브 트리의 수 +1) ~ 11(끝 인덱스) = 8 ~ 11
=> 왜냐! root가 중간에 있으니!
후위 순회에서 왼쪽 서브 트리의 범위는
시작 인덱스 ~ (시작 인덱스 + 왼쪽 서브 트리의 노드 수 -1)
ex) 0(시작인덱스) ~ 0+7-1(시작 인덱스 + 왼쪽 서브 트리의 노드 수 -1) = 0 ~ 6
후위 순회에서 오른쪽 서브 트리의 범위는
(끝 인덱스 - 오른쪽 서브 트리의 수) ~ (끝 인덱스-1)
ex) 11-5+1(끝 인덱스 - 오른쪽 서브 트리의 수 +1) ~ 11-1(끝 인덱스-1) = 7 ~ 10
=> 왜냐 ! root가 마지막에 있으니 !
# 2263: 트리의 순회
# https://ku-hug.tistory.com/135?category=978336
# 후위 순회에서 부모 노드를 찾아 중위 순회에서 기준으로 삼아 왼쪽, 오른쪽으로 나눈다.
# 그리고 왼쪽 자식 트리 노드, 오른쪽 자식 트리 노드를 순회하며 앞의 과정을 반복한다.
# 이해할 듯 모르겠다................................
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n = int(input())
in_order = list(map(int, input().split()))
po_order = list(map(int, input().split()))
pre = [0] * (n+1)
for i in range(n):
pre[in_order[i]] = i
def preorder(in_start, in_end, po_start, po_end):
if (in_start > in_end) or (po_start > po_end):
return
root = po_order[po_end] # 후위순회의 마지막 인덱스에 루트가 있다.
print(root, end=" ")
# 왼쪽 서브 트리의 노드 수
left = pre[root] - in_start
# 오른쪽 서브 트리의 노드 수
right = in_end - pre[root]
preorder(in_start, in_start+left-1, po_start, po_start+left-1)
preorder(in_end-right+1, in_end, po_end-right, po_end-1)
preorder(0, n-1, 0, n-1)# 2263: 트리의 순회
# https://backtony.github.io/algorithm/2021-02-17-algorithm-boj-class4-17/
# n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복없이 매겨져 있다.
# 1. 트리 전체에서 보면 후위 순회의 제일 마지막 값은 루트 노드에 해당한다.
# 2. 중위 순회에서 루트 노드에 해당하는 값의 인덱스를 기준으로 보면 왼쪽은 루트노드 기준 왼쪽 서브 트리, 오른쪽은 오른쪽 서브트리에 해당한다.
# 3. 전위 순회 출력이 목적이므로 현재의 루트를 찍고 왼쪽부터 재귀 반복, 오른쪽 재귀 반복한다.
# 모오오오오르겠다 ^^
import sys
sys.setrecursionlimit(10**6)
sys.stdin = open("RETRY/트리의순회/input.txt","r")
input = sys.stdin.readline
def preorder(in_left, in_right, po_left, po_right):
# 역전되면 구분할 노드가 없는 것
if in_left > in_right or po_left > po_right:
return
root = postorder[po_right]
print(root, end=" ")
left = idx[root] - in_left # 왼쪽 개수
right = in_right - idx[root] # 오른쪽 개수
# 전위이므로 루트찍고 왼쪽부터
preorder(in_left, in_left+left-1, po_left, po_left+left-1)
# 오른쪽
preorder(in_right-right+1, in_right, po_right-right, po_right-1)
n = int(input().rstrip())
inorder = list(map(int, input().split())) # 중위 순회
postorder = list(map(int, input().split())) # 후위 순회
idx = [0] * (n+1)
# 후위순회의 끝값이 중위 순회의 어디 인덱스에 위치한지 확인을 위해
# 중위순회의 값들의 인덱스 값을 저장
for i in range(n):
idx[inorder[i]] = i
preorder(0, n-1, 0, n-1)
공부 참고 블로그:
From DL GITHUB CODE
From YJ Explain
'Problem Solving > Algorithm Concepts' 카테고리의 다른 글
| [알고리즘] 유클리드 호제법 & 백준(최대공약수와 최소공배수) (0) | 2022.12.13 |
|---|---|
| [알고리즘] BFS 뿌셔 DFS 뿌셔 (0) | 2022.10.10 |
| [알고리즘] 그래프와 트리, 전위순회, 중위순회, 후위순회& 백준(트리 순회) (1) | 2022.10.08 |
| [알고리즘] 스택 & 백준(탑, PPAP) (0) | 2022.10.08 |
| [알고리즘] 이분 탐색, 투 포인터 알고리즘 & 백준(두 수의 합, 두 용액) (1) | 2022.10.06 |

