BFS
- BFS = Breath-First Search
- 가까운 노드부터 우선 탐색
: s로부터 거리가 k+1인 한 정점을 만나기 전에, s로부터의 거리가 k인 정점을 모두 발견하는 알고리즘 (CLSR에 적힌 정의)
- 큐 자료구조를 이용:
1. 탐색 시작 노드를 큐에 삽입, 방문 처리
=> Queue에 들어있는 애들 = frontier
2. 큐에서 노드를 꺼낸 뒤 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
=> frontier 갱신
1) 큐에서 popleft() (popleft()한 값 u / deque이기 때문에 popleft()를 통해서 큐의 맨 앞 요소를 빼줌)
2) u의 인접 노드 v 를 방문했는지 확인
3) 방문 안 했으면 큐에 v 삽입 + v의 dist 값 업데이트(u의 dist + 1) + 방문처리
3. 더 이상 2를 수행할 수 없을 때까지 반복
- 특정 조건에서 최단거리 경로 문제를 해결하기 위해 많이 사용
- 간선의 비용이 동일하다면 거리에 총 비용이 비례하기 때문에 bfs를 최단거리 경로를 구하는 목적으로 사용가능하다.
- 우선순위 큐도 활용가능 (min-heap 사용) => 같은 비용의 목적지를 오름차순으로 출력 가능
- 큐, 우선순위 큐 사용법
from collections import deque # import deque for 'Queue'
import heapq # import heapq for 'Priority Queue'- BFS 구현
# BFS
from collections import deque
# 각 노드가 연결된 정보를 표현 (2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# 각 노드가 방문된 정보를 표현 (1차원 리스트)
visited = [False] * 9
# BFS 메서드 정의
def bfs(start):
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력하기
u = queue.popleft()
print(u, end=" ")
# 아직 방문하지 않은 인접한 원소들을 큐에 삽입
for v in graph[u]:
if not visited[v]:
visited[v] = True
queue.append(v)
# 정의된 BFS 함수 호출
# 실행 결과: 1 2 3 8 7 4 5 6
bfs(1)DFS
- DFS = Depth-First Search
- 스택 자료구조 혹은
- 재귀함수를 이용:
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드 꺼냄
3. 더이상 2번을 수행할 수 없을 때까지 반복
- 스택으로 하는 법 ✨
=> bfs랑 비슷한 구조로 큐 대신 스택을 사용
첫 애 친구들이 a, b, c 순서면 재귀로 할 땐 a 친구의 친구의 친구의 친구로 시작하는데 스택으로 하면 a,b, c 넣어두고 c를 넣다가 빼고 걔친구 넣다가 빼고 해서 방문 순서가 다르다. reverse를 활용하면 동일하게 방문 가능함.
# DFS
# 각 노드가 연결된 정보를 표현 (2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# 각 노드가 방문된 정보를 표현 (1차원 리스트)
visited = [False] * 9
# DFS 메서드 정의
def dfs(start):
# 현재 노드를 방문 처리
visited[start] = True
print(start, end=" ")
for node in graph[start]:
if not visited[node]:
dfs(node)
# 정의된 DFS 함수 호출
# 실행 결과: 1 2 7 6 8 3 4 5
dfs(1)아래부터는 삽질의 현장이다................
- 삽질 덕에 스택으로 DFS를 구현하는 방법에 대해 알게됨.
- 함수 인자에 graph를 굳이 넣어주지 않아도 global로 인식하게 됨.
- visited = [False] * (N+1) 이런 식으로 외부에서 선언하고 함수 안에서 visited[start]=True로 방문처리 해주면 됨.
너비 우선 탐색(BFS, breadth-first search)
- 한 단계씩 내려가면서, 해당 Node와 같은 레벨에 있는 형제 노드를 먼저 탐색
- 너비 우선 탐색(BFS)는 2개의 queue가 필요하다.
- need_visited: 방문 예정인 방문 대기 queue (순서가 매겨져 있음)
- visited: 방문 완료 queue (순차적으로 방문함)
- 방문 대기 queue(need_visited)에서 앞에서부터 하나씩 빼서 이미 방문하였다면 스킵하고, 방문하지 않았다면 방문 완료 queue(visited)에 추가한 뒤, *추가된 Node에서 갈 수 있는 Node를 방문 대기 queue(need_visited) 뒤 편에 줄을 세운다.
* 추가된 Node에서 갈 수 있는 Node 예시
graph['B'] = ['A', 'D'] => B Node에서 갈 수 있는 노드는 A Node와 B Node이다.
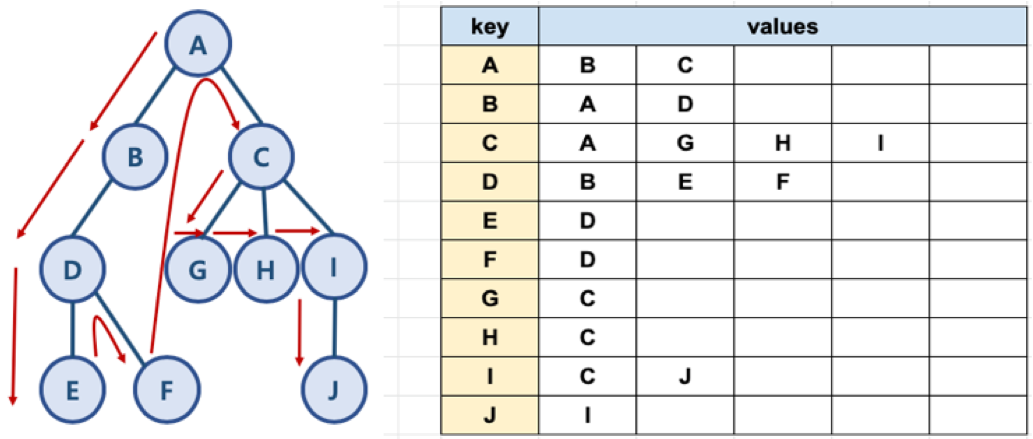
# BFS: 너비 우선 탐색
from collections import deque
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
def bfs(graph, start):
# visited: 방문 완료한 queue 생성
# need_visited: 방문 대기열 queue 생성
need_visited, visited = [], []
# start를 맨 처음 방문 대기열에 추가
need_visited.append(start)
# 방문 대기열이 없을 때까지
while need_visited:
# 방문 대기열의 맨 처음 요소를 제거하고 node에 담음
node = need_visited.pop(0)
# node가 방문 완료 queue에 있는지 확인
if node not in visited:
# 없으면 방문 완료 queue에 추가
visited.append(node)
# node와 연결된 Node들을 대기열에 추가
need_visited.extend(graph[node])
return visited
print(bfs(graph, 'A'))
# ['A', 'B', 'C', 'D', 'G', 'H', 'I', 'E', 'F', 'J']- BFS에서 Node의 수를 V, 간선의 수를 E라고 할 때, 시간 복잡도는 O(V+E)
- BFS는 queue를 이용해 구현하고, 갈 수 있는 곳을 전부 queue에 넣은 후 queue의 앞에서부터 하나씩 빼서 탐색하는 방식이다.
- 즉, 갈림길마다 기준에 맞추어 경로를 queue에 넣은 후, 먼저 추가된 경로(우선 순위 높은 경로)를 차례대로 탐색한다.
깊이 우선 탐색(DFS, depth-first search)
- 탐색할 수 있을 때까지 깊게 탐색하고, 더이상 탐색할 대상이 없으면 갈림길이 존재하는 지나친 최근 노드로 돌아와 아래로 탐색하는 방식(정점의 자식들을 먼저 탐색)
- 깊이 우선 탐색(DFS)는 1개의 stack과 1개의 queue가 필요
- need_visited: 방문 예정인 방문 대기 stack (순서가 매겨져 있음)
- visited: 방문 완료 queue (순차적으로 방문함)
- BFS는 방문 대기 queue에 추가하고 먼저 추가된 Node부터 꺼내어 이미 방문하였는지 확인하는데 반해, DFS는 방문 대기 stack에 추가하고 가장 나중에 추가된 Node부터 꺼내어 이미 방문하였는지 확인하는 차이가 있다.

# DFS: 깊이 우선 탐색
from collections import deque
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
def dfs(graph, start):
# visited: 방문 완료한 queue 생성
# need_visited: 방문 대기열 stack 생성
need_visited, visited = [], []
# start를 맨 처음 방문 대기열에 추가
need_visited.append(start)
# 방문 대기열이 없을 때까지
while need_visited:
# 방문 대기열의 마지막를 제거하고 node에 담음
node = need_visited.pop()
# node가 방문 완료 queue에 있는지 확인
if node not in visited:
# 없으면 방문 완료 queue에 추가
visited.append(node)
# node와 연결된 Node들을 대기열에 추가
need_visited.extend(graph[node])
return visited
print(dfs(graph, 'A'))
# ['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']
print()
# 특징적인 것은 visited 자료형을 기본 함수 인자로 포함시키고,
# 방문한 리스트들을 재귀함수를 통해 visited에 담는 방식
def dfs_recursive(graph, start, visited=[]):
visited.append(start)
for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited
print(dfs_recursive(graph, 'A'))
# ['A', 'B', 'D', 'E', 'F', 'C', 'G', 'H', 'I', 'J']- DFS에서 Node의 수를 V, 간선의 수를 E라고 할 때, 시간 복잡도는 O(V+E)이다.
- DFS는 재귀함수 또는 stack을 이용해 구현하는데 보통 재귀함수로 구현하는게 더욱 간편하다.
=> DFS를 살펴보면 결국엔 전위순회, 중위순회, 후위순회 모두 DFS이다.
[알고리즘] 그래프와 트리 & 백준(트리 순회)
그래프 그래프는 현상이나 사물을 정점(Vertex) 또는 노드(Node), 간선(Edge)으로 표현하기 위해 사용한다. - 노드(Node) : 위치를 말함, 정점(Vertex)라고도 함 - 간선(Edge) : 위치 간의 관계를 표시한 선으
bo5mi.tistory.com
공부 참고한 블로그:
직관적인 BFS 설명: https://chanhuiseok.github.io/posts/algo-27/
상단 DFS, BFS 설명 참고 From WH: https://velog.io/@wonhee/%EA%B7%B8%EB%9E%98%ED%94%84-%EA%B8%B0%EB%B3%B8-%EA%B0%80%EB%A3%A8%EB%B0%95%EC%82%B4
'Problem Solving > Algorithm Concepts' 카테고리의 다른 글
| [알고리즘] 유클리드 호제법 & 백준(최대공약수와 최소공배수) (0) | 2022.12.13 |
|---|---|
| [알고리즘] 이진 트리, 이진 검색 트리 & 백준(이진 탐색 트리, 트리의 순회) (2) | 2022.10.12 |
| [알고리즘] 그래프와 트리, 전위순회, 중위순회, 후위순회& 백준(트리 순회) (1) | 2022.10.08 |
| [알고리즘] 스택 & 백준(탑, PPAP) (1) | 2022.10.08 |
| [알고리즘] 이분 탐색, 투 포인터 알고리즘 & 백준(두 수의 합, 두 용액) (2) | 2022.10.06 |

